能量消耗有多種，如靜息能量消耗（resting energy expenditure，REE）、基礎能量消耗（basal energy expenditure，BEE）、 每日靜息能量消耗（resting daily energy expenditure，RDEE)、每日總能量消耗（total daily energy expenditure，TDEE）等，準確預測人體能量需求是實施營養健康咨詢及臨床營養支持的先決條件。

能量需求的預測方法有兩類 ：①測定法（measurement），即測定每日能量消耗（measured daily energy expenditure，MDEE），具體方法有量熱計（calorimeter）直接測熱法、代謝車間接測熱法（metabolic cart indirect calorimetry）；②估算法（estimation），即估算每日能量消耗（estimated daily energy expenditure，EDEE），具體方法是用公式計算。

直接測熱法既昂貴又復雜、只能在實驗研究中使用 ；間接測熱法基層單位難以普及。估算法雖然沒有測定法精確，但是簡易、方便、價廉。目前行業已發表的估算公式共有 200 多種，分別估算不同條件下的能量消耗及需求 。本文介紹幾種常用的估算法，并分析不同公式的優缺點及其適用人群。

一、Harris-Benedict 方程式

Harris-Benedict 方程式（Harris-Benedict equation，HBE）可能是人類歷史上第一個 REE 預測公式，測定法及其它估算法均在其后。HBE 始建于 1919 年，是在 239 例健康成年人（男女分別為 136、103 例）的數據基礎上形成的，包括年齡、性別、身高及體重 4 個基本變量。在計算 TDEE 時還要考慮活動、發熱、創傷及營養不良等附加因素。原始 HBE 如表 1。

研究發現 HBE 偏向（適用）于營養良好的青年人及非肥胖人群，其估算值比間接測熱法測定值高 6%~15%。

Garrel DR 等報告一組 67 例健康志愿者，HBE 計算值比測定靜息代謝率（resting metabolic rate，RMR）平均高 21％，其高估值大小與 RMR 高低呈負相關，即 RMR 越高，其高估值越小（越接近實際情況），RMR 越低，其高估值越大。所以， HBE 對 RMR 較低的女性及瘦體組織（lean body mas，LBM）減少的患者有很大的高估風險。

由于 HBE 個體差異較大，該公式對體重丟失、急慢性疾病、營養不良患者的價值有限 。對于腫瘤患者，Alpers D 等人建議在 HBE 計算值的基礎上乘以 1.3，用以估算腫瘤患者的 TDEE。但是，Bauer J 等報告，HBE 乘以 1.3 后其估算值顯著高于間接測熱法測定值。

二、Cunningham 公式

1980 年 Cunningham JJ 利用 Harris JA 及 Benedict FG 的 239 例受試者的原始數據，排除 16 例運動員的數據后，回歸分析發現 LBM 是基礎代謝率（basal metabolic rate，BMR）的唯一顯著有效預測因素，年齡、性別、身高及體重均是 LBM 的影響因素，與 BMR 無明顯直接關系。因此，得出基于 LBM 的公式如表 2。

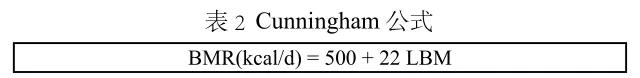
公式中的LBM計算方法是Moore FD等人1963年建立的，具體見表 3。

2014 年 ten Haaf T 及 Weijs PJ 報 告 ，Cunningham 公式能夠準確預測運動員（recreational athlete）的能量需求，而HBE、FAO/WHO/UNU、Mifflin 及 Owen 公式對該人群的預測準確性均低于 50%。

三、Shizgal-Rosa 方程式

鑒于 HBE 的缺陷，1984 年 Roza AM 及 Shizgal HM 用 Harris JA 及 Benedict FG 當年的原始數據結合新的數據，對原始 HBE 進行了重新評價與修訂，改良后的 HBE 如表 4，又稱為 Shizgal-Rosa 公式。研究發現，該公式與實際能量消耗更加接近，更加準確。在 1990 年 The Mifflin-St Jeor 公式出現之前，Shizgal-Rosa 方程式是最為準確的 REE 預估公式。

在對體重、身高、年齡、性別及體細胞群（bodycell mass，BCM）進行綜合分析后，Roza AM 及 Shizgal HM 發現，傳統 HBE 的年齡、性別、身高及體重 4 個變量實際上都與 BCM 密切相關，或者說可以由 BCM 替代，所以，他們又提出了基于 BCM 的另外一個 REE 計算公式，如表 5。

四、Owen 方程式

1986 年 Owen OE 等用間接測熱法測量了 44 例 18~65 歲，體重 43~143 kg 健康女性的能量消耗，其中有 8 位運動員。多因素回歸分析發現，只有體重與 RMR 關系最為密切，而且運動員與非運動員有顯著差別。由此，他們建立了 Owen 方程式，見表 6。

Hasson RE 等對 362 名 18~60 歲成年人的研究發現，Owen 方程式比較適用于 50~60 歲年齡組的人群。Siervo M 等人對 157 例青年白人婦女的研究發現，Owen 公式適用于指導體重正常青年女性的營養咨詢。

五、Mifflin-St Jeor 公式

1990 年 Mifflin MD 等人提出了一個更好的 REE 計算公式，如表 7。

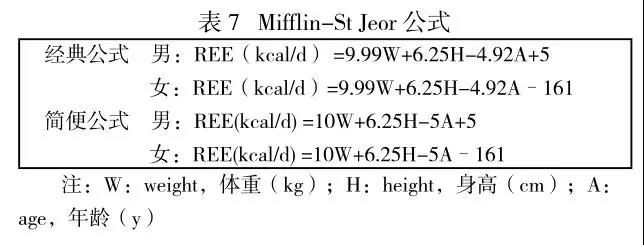
在系統分析的基礎上，2005 年美國營養師學會（The American Dietetic Association，ADA） 認為 Mifflin-St Jeor 公式是目前計算 REE 的最佳方法，2008 年美國臨床營養學會（American Society for Clinical Nutrition，ASCN）官方雜志 —《美國臨床營養雜志》有同樣的推薦報告 。Mifflin-St Jeor 公式對普通成年人 REE 的評估誤差率在 10％ 以內，但是該公式對老年人及不同種族人群有一定的差異，該公式不適用于只有肌肉而沒有脂肪的舉重運動員。

六、WHO/FAO/UNU 公式

1985 年 WHO/FAO/UNU 提出了他們基于體重以及基于體重及身高的兩個 BMR 計算公式，表 8。

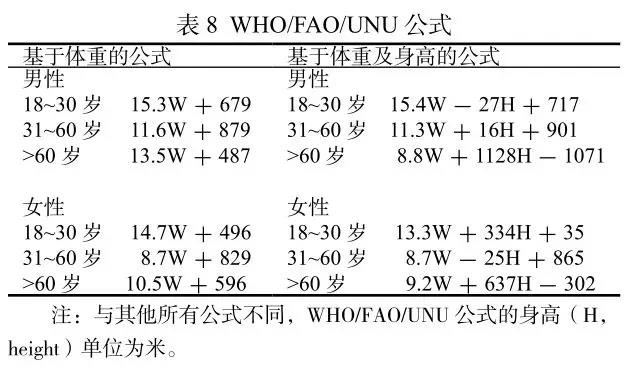
WHO/FAO/UNU 公式的數據主要來源于年輕的歐洲軍人及警察，男性 2279，女性 247。盡管年齡在 19~82 歲之間，但是，實際上老年人很少。研究報告 WHO/FAO/UNU 公式對老年人的 RMR 預測不夠精確，低估與高估并存，而且不適合肥胖人群 。

TDEE 是指一天（24 小時）的總能量消耗，包括休息時的能量消耗及活動時的能量消耗兩個部分，其中前者占 2/3（REE 相當于 TDEE 的 60％~80％），后者占 1/3。WHO/FAO/UNU 根據個體活動情況將 TDEE 分為 6 類 ：①非常不活動但并非臥床者，TDEE=REE× 1.2 ；②不活動（很少或沒有運動，辦公室工作）者，TDEE=BMR×1.2 ；③輕度活動（每周 1~3 天輕度活動 / 運動）者，TDEE=BMR×1.375 ；④中度活動（每周 3~5 天中度活動 / 運動）者，TDEE=BMR× 1.55 ；⑤重度活動（每周 6~7 天重度活動 / 運動）者，TDEE=BMR×1.725 ；⑥超重活動（極重的活動 / 運動，重體力勞動或每天 2 次訓練如馬拉松、競賽等）者，TDEE= BMR×1.9 。

七、拇指法則（rule-of-thumb，ROT）

經典的拇指法則是每日能量需求為 25kcal/kg，傳統上，25kcal/kg 的計算值是活動患者的 REE 或不活動患者的 TDEE，其中的體重為理想體重。由于每日能量需求受年齡、性別、BMI、運動及應激等因素的影響，所以 ROT 值不應該是一個恒定數值，而應該動態調整。

隨著體重增加，ROT 值應該下調，因為增加的體重是脂肪組織，而脂肪組織是非活躍器官。Zauner A 等建議對體重正常、超重、肥胖、病態（嚴重）肥胖患者分別使用 25kcal/kg、22kcal/kg、20kcal/kg、16kcal/kg 計算其 REE。同樣，隨著年齡的增加，成年后每 10 年 REE 下降 1%~2%，ROT 也應該下調，因為肌肉逐漸減少，而脂肪組織的比例相對升高。

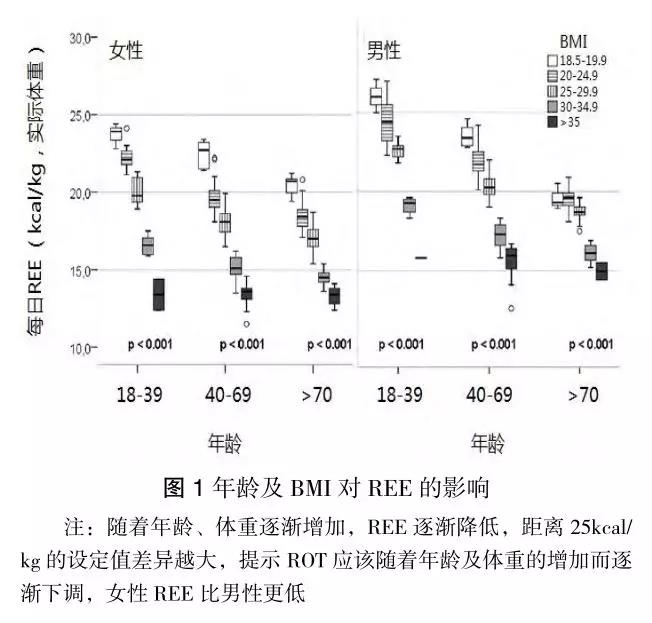
Valentini L等對 5 家醫院 676 例連續入院患者用 HBE 計算其 REE，發現即使采用理想體重計算，ROT 的 25kcal/kg 也高估了 95% 患者的能量需求，而且隨著年齡增加、隨著體重增加，其高估值越大，而且還有顯著的性別差異，圖 1。有鑒于此，ESPEN 2009 指南推薦 25kcal/kg 是患者的 TDEE，而不是 REE，只有在極少數嚴重應激狀態下，才需要 30kcal/kg 。Valentini L 等還建議，創傷、疾病等應激條件下計算 TDEE 時，根據年齡、性別及體重調整后的 REE 應該乘以應激系數，但是主張降低傳統的應激系數數值，將系數根據應激輕、中、重分為 1.1、1.2 及 1.3 三個等級，見表 9。

八、人體成分估算法

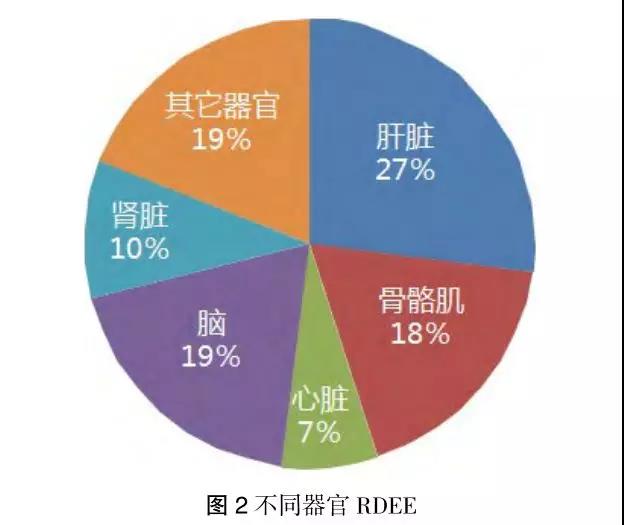
根據代謝率不同，人體組成可以分為8個部分，即腦、心、肝、腎、骨骼肌、骨骼、脂肪組織及其他組織，其能量需求（消耗）各不相同，骨骼為 2.3kcal/（kg?d），骨骼肌為 14.5kcal/（kg?d），脂肪組織為 13kcal/（kg?d），腎臟、心臟為 440kcal/（kg?d），腦 240kcal/（kg?d），肝臟 200kcal/（kg?d）。腦、肝、心、腎盡管占全部體重不足 6％，但是其總能量消耗占 REE 的 60%~70%，骨骼肌盡管占全部體重的 40%~50%，但是其能量消耗只占 REE 的 20%~30% 。不同器官組織的耗能比例見圖 2。

根據不同組織、器官的代謝率，Elia?M  提出了一個 REE 計算（Calculation?of?REE，REEc) 公式，見表 10。

人體成分估算法沒有實際操作價值，但是它對理解腫瘤條件下的能量消耗有重要意義。腦、肝、心、腎為高代謝器官，其重量的微小變化可以導致能量消耗的顯著變化，腦、肝、腎的原發腫瘤或繼發腫瘤增加了所在器官的重量，使得所在器官能量消耗顯著增加，機體處于高代謝狀態，能量負債加大，進而導致營養不良及惡液質。

能量需求的準確預測是臨床營養支持的前提。測定法雖然相對精準，但是其操作復雜、價格不菲、要求患者空腹休息等待時間長，而且中國幅員遼闊，差異巨大，醫院條件及患者病情不同，所以能量估算法有巨大的應用空間。而且，隨著手機及 iPad 廣泛使用，估算法將變得更加便利。盡管每一種估算法各有優缺點，研究結果參差不齊，但是 Mifflin-St Jeor 公式得到 ADA、ASCN 的一致推薦。

鑒于體重差異巨大，在實際應用過程中，應該對體重進行校正。對體重在正常范圍內的人群，實際體重與理想體重基本一致，可以選擇實際體重估算能量需求 ；對肥胖人群，選擇實際體重會高估能量需求，選擇理想體重會低估能量需求 ；Glynn CC 等推薦選取實際體重及理想體重的平均值進行估算。需要指出的是，上述所有估算法均是基于正常人群的數據，疾病情況下特別是腫瘤條件下的能量消耗與需求的估算仍然有待研究。

來源：石漢平醫生